Batch 3 - Class 241 - Logic, Truth Tables

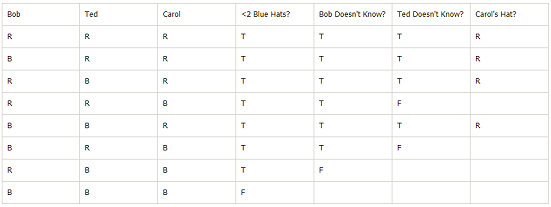
• A real puzzle with truth tables - Bob, Ted,and Carol play a hat game. This particular game is played with 5 hats, three red, and two blue. Each person gets one hat put on his or her head. Bob can see Ted’s hat and Carol’s hat but can’t see his own. Ted can see Bob’s hat and Carol’s hat, but not his own. Carol cannot see any of the hats. The game is to see which player is the first to figure out what color hat he or she is wearing. Bob goes first. He says he can’t tell. Then Ted says he can’t tell. Carol now says she is wearing a red hat. How did she know?
• Draw the equivalent of truth table for this (instead of T and F, it will be color of hats - first draw all possibilities, then start to reduce possibilities)
• "Constraining the truth table" can provide answers
• Answer: Notice that in the final analysis, all four possibilities have Carol wearing the Red Hat

  

• Example:  All humans are mortal. Socrates is a human. What can we infer about mortality of Socrates?
• Answer: Therefore Socrates is mortal.
• Subject of conclusion is the "Minor term", Predicate is the "Major term" and the common word is "Middle term"
• Example: No reptiles have fur. All snakes are reptiles. What can we infer about snakes and furs?
• Answer: No snakes have fur.
• Example: All rabbits have fur. Some pets are rabbit. What can we infer about pets having fur?
• Answer: Some pets have fur.
• Example: No homework is fun. Some reading is homework. What can we infer about reading being fun?
• Answer: Some reading is not fun.
• Example: All informative things are useful. Some websites are not useful. What can we say about websites being informative?
• Answer: Some websites are not informative.

• Draw a truth table for one variable, like human - two values truth and false
• Draw a truth table for two variables, like human and mortal - 4 values in all
• Which rows of the truth table support the statement "All humans are mortal"
• If "Socrates is human", then what must the value of mortal be
• Introduce the notion of A implies B - draw the truth table. For "A and B", "A or B"
• What does "A implies B" say about things which are not A?
• Introduce notion of negation
• What is the value of "Not A" for all values of A?
• MathElem: Chapter 10 - Game of "Yep" and "Nope" clowns
• Yep says "All kids go to school"
• Nope says "Some kids do not go to school" (Careful about "Some kids go to school" or "All kids do not go to school"
• Yep says "All princesses wear pink"
• Nope says "Some princesses do not wear pink" (Careful about "All princesses do not wear pink")
• Match Yep statements on left with Nope statements on right
• 
• Expression Evaluation - Revision
• What rows correspond to not (A implies B)?
• Give a more complex formula such as evaluation of (A and not B or C or not (D and E and F)) for A, B, D, E true and C, F false
• Prove that (A implies B) is same as (not A or B)
• Prove that not (A or B) is same as not A and not B (De Morgan's Law)
• Knights and Knaves - Two people from the island, A and B
• A says "I am Knave and B is knight" - who is who (Draw truth table, with T and F signifying Knight and Knave)
• A says "Both of us are Knights" and B says "A is lying and 2+2=4" - who is who?
• A says "If B is a knight then I am a knave" - who is who?

• (Waterloo - Problem 11) There is a secret hall at Hogwart’s with magical closets. When you open a closet door, you might find Harry Potter, or you might find Voldemort. Since Hogwarts is magic, it is possible that both doors contain Harry Potter, or both doors contain Voldemort. 
• (a) When you enter the secret hall, you encounter two closet doors. “One of the signs is true,” says Professor Snape,“and the other is false.”  
• i. First Door: Harry is behind this door. Voldemort is behind the other.
• ii. Second Door: Harry is behind one of these doors. Voldemort is behind the other.
• Who is behind each door? 

• Who is behind each door?